Demostración de derivadas de funciones exponenciales y funciones logarítmicas
A continuación vamos a demostrar las derivadas de las funciones exponenciales y logarítmicas.
 , por la definición de derivada:
, por la definición de derivada:
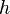 tiende a cero
tiende a cero  tiende a infinito, podemos hacer el siguiente cambio de variable:
tiende a infinito, podemos hacer el siguiente cambio de variable:
 .
.
 . Vamos a usar la derivada de la función inversa:
. Vamos a usar la derivada de la función inversa:
 y
y  són funciones inversas, tenemos que:
són funciones inversas, tenemos que:
 , tenemos que:
, tenemos que:
 .
.
Vídeo Explicativo:
Derivada de la función logarítmica
Tenemos una función , por la definición de derivada:
, por la definición de derivada: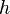 tiende a cero
tiende a cero  tiende a infinito, podemos hacer el siguiente cambio de variable:
tiende a infinito, podemos hacer el siguiente cambio de variable: .
.Derivada de la función exponencial
Partimos de una función exponencial . Vamos a usar la derivada de la función inversa:
. Vamos a usar la derivada de la función inversa: y
y  són funciones inversas, tenemos que:
són funciones inversas, tenemos que: , tenemos que:
, tenemos que: .
.Vídeo Explicativo:


![\begin{align} \frac{d}{dx}\log_a x &= \lim_{h \to 0}\log_a \left[\left(1 + \frac {1} {\frac{x}{h}}\right)^{\frac{x}{h}}\right]^{\frac{1}{x}} \\
&= \frac{1}{x}\lim_{h \to 0}\log_a \left(1 + \frac {1} {\frac{x}{h}}\right)^{\frac{x}{h}}\\
&= \frac{1}{x} \log_a \left[\lim_{h \to 0} \left(1 + \frac {1} {\frac{x}{h}}\right)^{\frac{x}{h}}\right] \end{align}](http://upload.wikimedia.org/math/a/8/0/a80123f363e4c57fce3f1ada86af1780.png)




![[f^{-1}]^{\prime}(a)=\frac{1}{f^{\prime}[f^{-1}(a)]}](http://upload.wikimedia.org/math/e/f/0/ef01dbd93e684afe22c91db0ac3ab99f.png)
![\begin{align}\frac{d}{dx}a^x &= \frac{1}{[\frac{1}{x} \log_a (e)] \circ [a^x]}\\
&= \frac{1}{[\frac{1}{a^x} \log_a (e)]}\\
&= \frac{a^x}{\log_a (e)} \end{align}](http://upload.wikimedia.org/math/c/c/d/ccdc90d38229cd3da3d0d32cf656bac7.png)

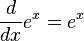
No hay comentarios:
Publicar un comentario